Cartan–Eilenberg resolution

In homological algebra, the Cartan–Eilenberg resolution is in a sense, a resolution of a complex. It can be used to construct hyper-derived functors.

Definition

Let 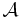be an Abelian category with enough projectives, and let A_∗ be a chain complex with objects in 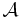. Then a Cartan–Eilenberg resolution of A_∗ is an upper half-plane double complex P_∗∗ (i.e., P_pq = 0 for q < 0) consisting of projective objects of 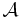and a chain map ε : P_p0 → A_p such that

• A_p = 0 implies that the pth column is zero (P_pq = 0 for all q).
• Taking the boundaries and homology of the pth column of P_∗∗ give projective resolutions of the pth boundary and homology groups of A_∗, respectively. In other words, one has chain complexes ε : P_p∗ → A_p, and applying the boundary and homology functors to these complexes turns them into projective resolutions.

There is an analogous definition using injective resolutions and cochain complexes.

The existence of Cartan–Eilenberg resolutions can be proved via the horseshoe lemma.

Hyper-derived functors

Given a right exact functor 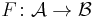, one can define the left hyper-derived functors of F on a chain complex A_∗ by constructing a Cartan–Eilenberg resolution ε : P_∗∗ → A_∗, applying F to P_∗∗, and taking the homology of the resulting total complex.

Similarly, one can also define right hyper-derived functors for left exact functors.

See also

• Hyperhomology

References

• Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, ISBN 978-0-521-55987-4, MR1269324